(A) グラフ描画アルゴリズムの設計
ここでいうグラフとは,頂点の集合と,頂点間を結ぶ辺の集合からなる構造のことです.グラフは実世界において
様々な構造や関係を表現するために用いられています.下図はその一例で,仮想的な科目間関係図を示したものです.
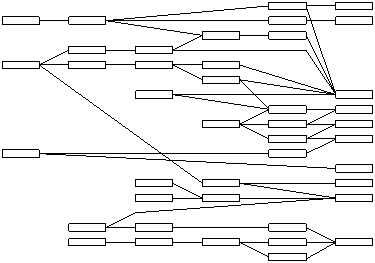
グラフ描画の例(科目間関係図)
この図では,頂点を長方形で,辺を長方形間の直線分あるいは折れ線で描いています.各頂点は授業科目を表しており,各辺は,それがつないでいる2つの科目が関連していることを意味しています.
グラフを適切に描画すると,それが表現している構造や関係の把握が容易になります.しかし,複雑な構造の
良い描画を求めることは,通常,非常に手間がかかる作業です.そのため,近年,グラフ自動描画アルゴリズムに
関する研究が国内外でさかんに行われてきています.
以下では,グラフ描画アルゴリズムに関しての研究内容を三つ簡単に紹介します.
(A-1) 力指向アプローチによるグラフ描画アルゴリズム
(A-2) 階層的描画を求めるアルゴリズム
(A-3) 頂点の位置関係を保存した直交描画を求めるアルゴリズム
いずれのテーマについても,現在も継続して研究を行っています.
(A-1) 力指向アプローチによるグラフ描画アルゴリズム
図1では頂点を長方形で描いていましたが,ここでは頂点を点で表します.また,頂点の位置を自由に決めることが
できるものとし,各辺は基本的に直線で描くこととします.力指向アプローチとは,頂点を質点,辺をバネとみなすことに
よって力学的モデルを考え,その収束状態を計算することによってグラフ描画を求めようとするものです.これまでに,
EadesやKamadaらによって,このアプローチによるグラフ描画アルゴリズムが提案されていました.
力指向アプローチをとる場合,頂点の初期位置と辺の理想長(バネの自然長に対応)を最初に定めます.理想長より
長い辺に対してはその端点の間に引力が,理想長より短い辺に対しては端点間に斥力が働きます.このような力を
計算する関数と計算の順序をうまく決めれば,グラフ描画アルゴリズムができます.本研究室では,辺でつながれている
頂点間だけでなく,辺でつながれていない2頂点間や頂点と辺の間に働く力を定義することによって,従来の方法より
質の高い描画を求めるアルゴリズムを開発しました.また,必要に応じて,折れ線や曲線を用いて辺を描くアルゴリズムも
設計しました.下の図は,本研究室で開発したアルゴリズムを規模の小さなグラフに対して実行した結果を示したものです.
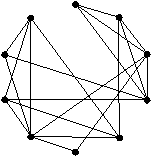
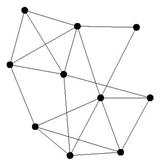
力指向アプローチによるアルゴリズムの実行例
[発表論文]
・ “折れ線や曲線を用いた無向グラフ描画アルゴリズム,” 電子情報通信学会論文誌(A), vol. J83-A, pp. 402-411 (2000).
・ “2種類の理想距離によるEadesのグラフ描画法の改良,” 電子情報通信学会論文誌(A), vol. J83-A, pp. 1117-1121 (2000).
・ “力指向グラフ描画アルゴリズムにおける頂点移動方法の改良,” 電子情報通信学会論文誌(A), vol. J91-A, pp. 974-982 (2008).
など
(A-2) 階層的描画を求めるアルゴリズム
頂点の集合をいくつかの部分集合に分割し,各部分集合の頂点を同じ垂直線(場合によっては水平線)上に置いてグラフを
描画したものを階層的描画と呼んでいます.このとき,階層とは,分割されてできた各部分集合のことを意味します.最初に示した
図中の描画は階層的描画であり,階層数は6です.階層的描画は,階層的な構造の表示や有向グラフを描画するためによく利用されます.
有向グラフの階層的描画を求めるアルゴリズムとしては,Sugiyanaらによる方法が代表的です.
このアルゴリズムは次の4段階よりなり,各段階で,ある評価基準に注目した最適化問題を発見的アルゴリズムにより解いています.
第1段階(グラフの非閉路化):できるだけ少ない本数の辺を選び,それらの向きを一時的に逆向きにすることによって,有向閉路のない
グラフにします.ここで一時的に逆向きにした辺は,最終的な描画で左向きの辺として描かれます(他の辺はすべて右向きの辺
として描かれます).
第2段階(頂点集合の階層への分割):各階層の頂点数の上限値が決まっているものとして,階層の個数ができるだけ少なくなるように,
頂点集合を階層に分割します.
第3段階(各階層上での頂点順序の決定):辺が交差する回数ができるだけ少なくなるように,各階層での頂点の配置順序を決定します.
第4段階(各頂点の座標の決定):各辺をできるだけ直線で描くことなどを目標として,各頂点の座標を決定します.その後,各辺を描きます.
上のアルゴリズムの各段階において,一つだけの評価基準に注目するのではなく,複数の評価基準を考慮することによって,最終的に
得られる描画の質を改善できる可能性があります.本研究室ではこれまでに,そのような試みを第1段階と第2段階に対して行いました.
この研究は現在も進行中です.
本研究室では,また,辺の描画段階についても,
² 辺を水平・垂直線分のみを用いて描くことにし,
² 複数の辺に対して,それらを構成する線分の共有を許す
ことによって,辺が交差する回数を従来の方法より大幅に削減できる描画アルゴリズムを開発しました.
[発表論文]
・ “局所探索法による階層的描画の辺交差削減” 電子情報通信学会論文誌(A), vol. J92-A, pp. 55-61 (2009).
・ “有向グラフ描画アルゴリズムにおける閉路削除法の改良,” 電子情報通信学会論文誌(A), vol. J92-A(6), pp.434-439 (2009).
・ “階層グラフ描画におけるダミー頂点の共有,” 電子情報通信学会論文誌(A), vol. J94-A, pp. 950-959 (2011).
・ “階層グラフ描画における頂点座標決定アルゴリズム,” 電子情報通信学会論文誌(A), vol. J94-A, pp. 960-073 (2011).
など
(A-3) 頂点の位置関係を保存した直交描画を求めるアルゴリズム
直交描画とは,グラフに対しある直交格子を考え,各頂点を格子点上に置き,各辺を格子上の垂直・水平線分からなる折れ線として
描いた描画です.鉄道の路線図や道路網の表示のために,路線や道路の形状を単純化したデフォルメ路線図やデフォルメ地図がよく
用いられています.これらの図で路線を描くときには,垂直・水平線分からなる折れ線がよく使われています.
本研究室では,グラフの描画が与えられたとき,それにおける頂点の相対的位置関係を基本的に保存し,どの辺の折れ曲がり回数も
高々4になるような直交描画を求めるアルゴリズムを開発しました.さらに,そのアルゴリズムに後処理を加えた方法を用いてデフォルメ
路線図作成をしてみました.下図にその実行例を示します.これは大阪市営地下鉄の路線図です.実際の駅の座標にしたがって頂点の
位置を決めたグラフ描画を入力として,開発したアルゴリズムによって直交描画を求めた後,路線ごとの色分けをしています.
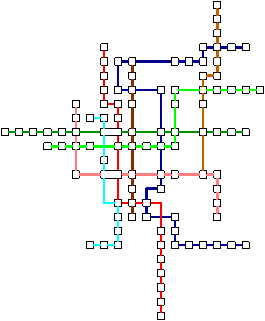
直交描画アルゴリズムにより作成したデフォルメ路線図
[発表論文]
・“グラフ描画の直交格子への埋め込みアルゴリズムとデフォルメ路線図作成への応用,” 電子情報通信学会論文誌(A), vol. J94-A, pp. 180-191 (2011).
