頂点彩色問題に対するRLF法の改良（工藤）

頂点彩色問題とは

無向グラフG=(V, E)に対し，任意の隣接する二頂点が異なる色を持つように各頂点に色を割り当てることをGの彩色といい，色数kによるGの彩色をGのk-彩色といいます．また，Gに対して色数kで彩色することができ，かつk未満の色数では彩色することができないとき，kをGの彩色数といいます．

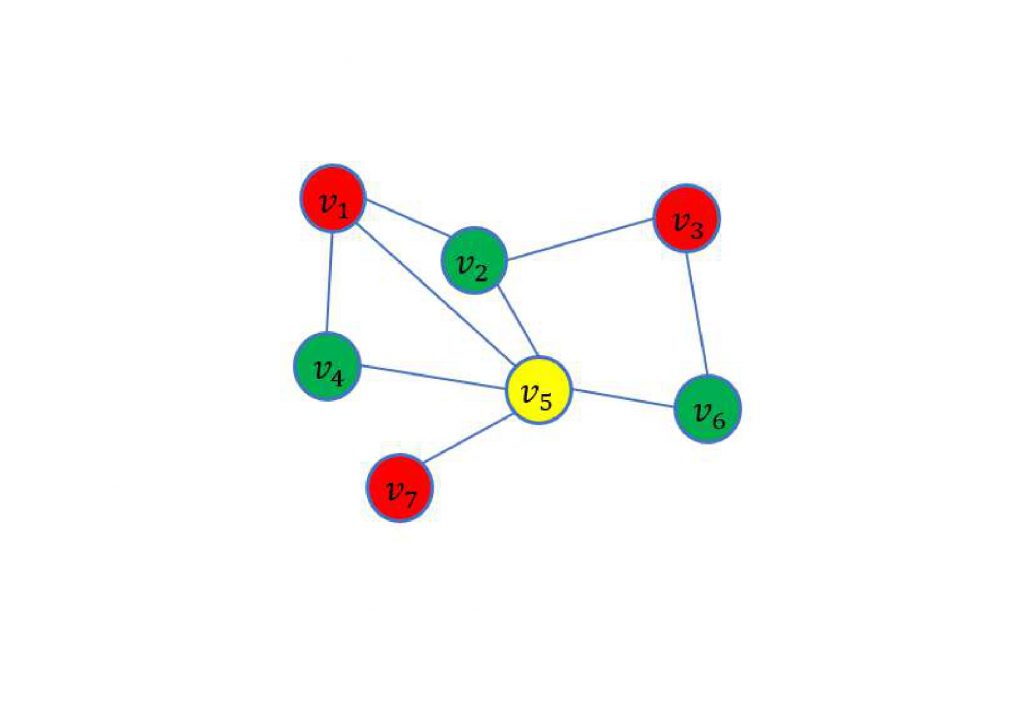
上の図はあるグラフの彩色例です．このグラフは3-彩色が可能であり，かつ2色で彩色できないため，彩色数は3です．グラフをできるだけ少ない色数で彩色する問題をグラフ彩色問題といいます．

グラフ彩色問題には，無線局への周波数割り当てやスケジューリング，タイムテーブリング，レジスタ割り当てなどの多数の応用例が知られています．一方で，グラフ彩色問題はNP-hard(難しい問題)であり，大規模なグラフの厳密解を求めるのは困難です．そのため，厳密解を得られる保証がない代わりに大規模なグラフに対しても高速に解を得ることができる発見的解法が求められています．

従来法と提案法

グラフ彩色問題には，代表的な発見的解法としてRLF法という手法があります．これは，独立集合の抽出を繰り返すことで彩色を行う手法です．独立集合を抽出する際に，元のグラフから削除できる辺の数が最大となるような頂点を選び，独立集合に加えていきます．

提案法では，各頂点をある色で塗ったとき，それと同じ色で塗れなくなる頂点の数が最小となるような頂点を考えました．この基準とRLF法の基準の線形結合を用い，これを基準として頂点を選び，独立集合に加えていく方法を提案しました．

計算機実験と評価

計算機実験において，提案法および代表的な貪欲法であるRLF法を実装し，48種類のDIMACSベンチマークに適用しました．実装の際には，線形結合の各項の係数をパラメータとして，様々なパターンを調べられるよう工夫しました．

その結果，パラメータを適切に選んだ場合，多くのインスタンスに対して提案法は解の質に関してRLF法よりも優れた結果を得ることができました．特に，パラメータの比率として，入力グラフの辺密度が～0.30の値のときには4，辺密度が0.30～の値のときには1/5, 1/4という値を採用すると，他のパラメータの場合と比べて質のより良い解を得られることを確認しました．