グラフ彩色問題に対する独立集合抽出型アルゴリムの開発 (明石健太郎)
グラフ彩色問題とは
与えられた無向グラフGに対して, 任意の隣り合う2頂点に同じ色を割り当てないように, 全ての頂点に色を割り当てることをGの彩色と呼びます. そして, Gをできる限り少ない色数で彩色する問題のことをグラフ彩色問題と呼びます. 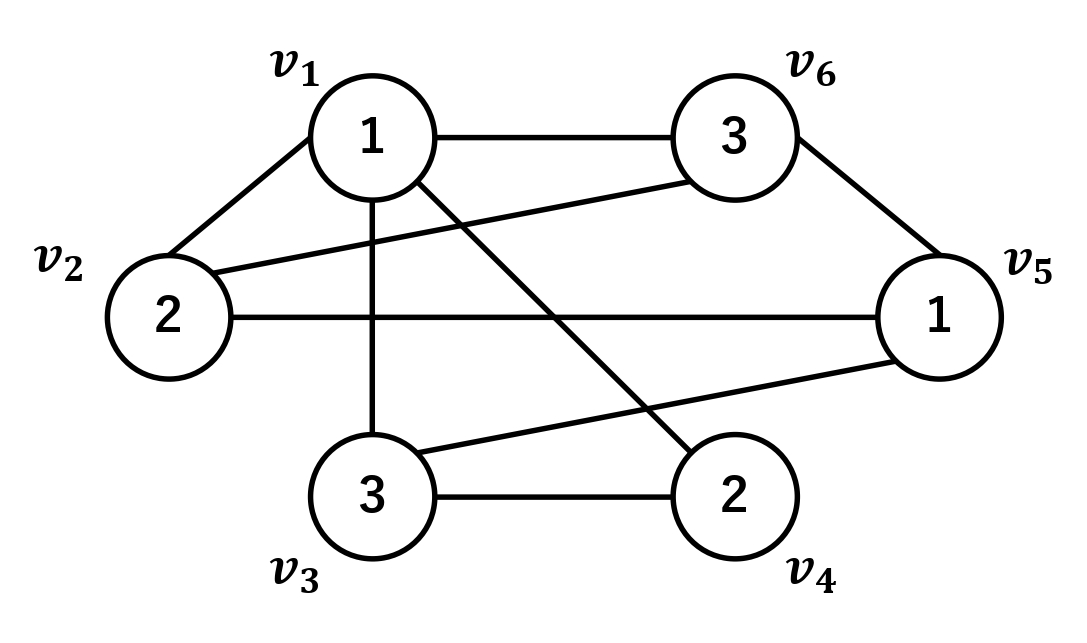
上の図の頂点の内部に表されている数字は, その頂点に割り当てられた色の色番号となります. 図中のグラフでは, 任意の互いに隣り合う2頂点に異なる色が割り当てられているので彩色されているといいます. また, このグラフは3色で彩色されていますが, 2色で彩色することはできないので, 彩色数の最小値は3となります.
グラフ彩色問題は, 多くの応用例が存在する重要な問題とされていますが, 大規模なグラフに対して, 厳密解を得るには膨大な時間を要します. (NP-hardという性質) よって, 多くの場合に必ずしも厳密解を得ることはできませんが, 短時間で上界を得ることができる発見的解法が用いられます. その中でもより高速に動作する貪欲法も多く用いられます.
目的とアプローチ
本研究では, 短時間で良質な解を得られる貪欲アルゴリズムの開発を目的としました. そのアプローチとしては, RLFという既存のアルゴリズムの改良を行いました.
RLFとはグラフ彩色に対する貪欲アルゴリズムの中でも, 高速で良質な解を得ることができると多く報告されている代表的な彩色アルゴリズムです. そのため, 多くの派生アルゴリズムも提案されています.
本研究では, RLFにビームサーチを用いて, 良質な解を得ることを目指しました. さらに, プログラムの並列化を行い, ビームサーチにより計算量の増加を抑制し, 高速で動作するアルゴリズムの開発を行いました.
計算機実験と評価
グラフ彩色アルゴリズムの性能を評価するためによく用いられるDIMACSベンチマークから抜粋した54種類のグラフを入力として用いて, RLFや提案アルゴリズムと類似の動作をするRLFの派生アルゴリズムとの性能を比較しました.
実験の結果, 提案アルゴリズムは高速で良質な解を得られるアルゴリズムであることが確認できました. 一方で, 派生アルゴリズムには少し性能が及ばなかった側面もありました.