巡回セールスマン問題の近似解法に関する実験的評価(池上)

巡回セールスマン問題

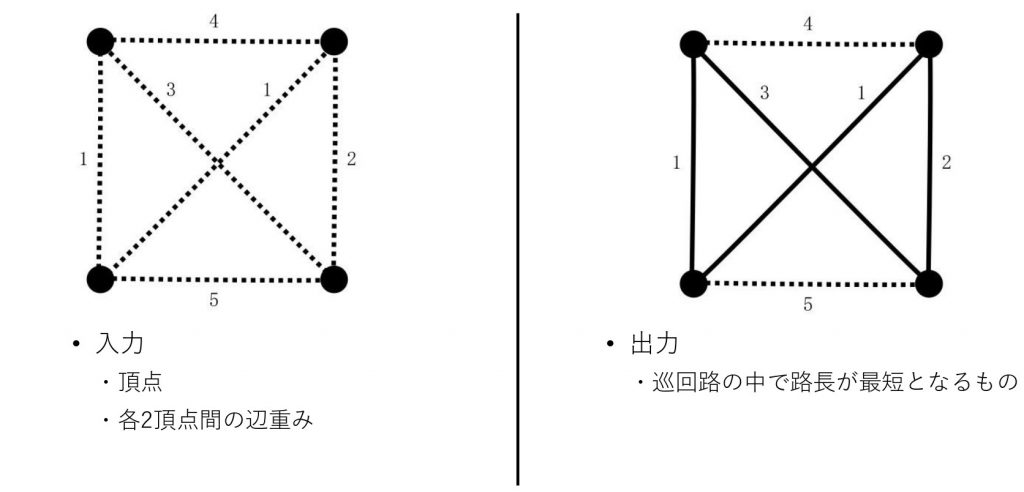
　巡回セールスマン問題とは，組み合わせ最適化問題の 1 つで，頂点と各 2 頂点間の辺の重みが与えられたとき，すべての頂点を一回ずつ通ったのち出発点となる頂点に戻る巡回路の中で路長が最短となるものを求める問題です．巡回セールスマン問題は，都市の数が多くなると多くの計算時間を要してしまうNP 困難な組み合わせ最適化問題の一つとなっています．

部品最適化法

　部品最適化法は，解が部品を組み合わせることによって構成されるという構造を利用したアルゴリズムです．このアルゴリズムは，最初に適当な巡回路を求め，それを部品に分解し，それらの部品の集合から構成された子問題に対し，厳密解法を適用して短い巡回路を得る手法です．今回の実験では，部品を連続したいくつかの頂点，また最初の巡回路を分割してできる部分グラフとした二つの手法について，従来法である2-opt法によって出力された巡回路と比較し性能を検証しました．以下の図に部品最適化法についての簡略図を記載しています（箱と矢印で巡回路を示しています）．

実験結果

　ランダムグラフに対して実験を行った場合，従来法に比べて部品最適化法による解は大きく劣るという結果が出ました．

　改善案として，部分グラフを部品とみなした場合においてスタート地点とゴール地点を固定していたのを，固定せずスタート地点とゴール地点を問わず巡回路を生成することが考えられます．